Introducción
En el siguiente trabajo que se muestra a continuación no es nada más ni nada menos que lo que explica el título del trabajo, matemáticas en las hojas de cálculo, en donde se explicara lo que es una hoja de cálculo y lo que es una función matemática, elementos importantes, para que se usa o de donde se obtienen y de qué manera se relacionan o están relacionados, de este tipo de cuestiones se verán a continuación.
También se encontraran con algunas definiciones de lo que es una variable, constante, rango y gráfico. Encontraran con la clasificación de funciones y un ejemplo de cada una de las funciones.
Por último en el trabajo se ve que esta un problema teórico y uno practico esto para enriquecer lo ya estudiado en este trabajo que sirve o te servirá en un momento dado de tu vida cotidiana.
Esto solo un adelanto de lo que veras a continuación.
¿Qué es una hoja de cálculo y que es una función matemática?
-Una hoja de cálculo (o programa de hojas de cálculo) es un software a través del cual se pueden usar datos numéricos y realizar cálculos automáticos de números que están en una tabla. También es posible automatizar cálculos complejos al utilizar una gran cantidad de parámetros y al crear tablas llamadas hojas de trabajo.
-En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).
¿Cómo se relacionan estos conceptos?
Que en las dos encontramos cálculos y para poder mostrar una función así ya gráficamente se requiere de una hoja de cálculo donde se obtendrán datos más exactos para su mayor comprensión.
Variable: Del latín variabĭlis, una variable es aquello que varía o puede variar. Se trata de algo inestable, inconstante y mudable. En otras palabras, una variable es un símbolo que representa un elemento no especificado de un conjunto dado. Este conjunto es denominado conjunto universal de la variable o universo de la variable, y cada elemento del conjunto es un valor de la variable.
Constante: Valores numéricos o de cadena que permanecen constantes, sin posibilidad de cambiar el valor que tienen.
Rango: es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.
Gráfico: es la manera de representar el esqueleto de un objeto, materia en 2 dimensiones.
"SU FORMA ANÁLITICA"
Función constante
Graficar la función f(x)=4, determinar su dominio y rango.
Se utilizara una tabla para poder ubicar las coordenadas de algunos puntos de la función.
x | f(x)=4 |
-2 | 4 |
-1 | 4 |
-0 | 4 |
1 | 4 |
2 | 4 |
Si observas la tabla se eligen los valores de la variable más comunes como -2, -1, 0, 1, 2, y a todos ellos al sustituirlos en l función se les asigna el 4.
Como su nombre lo dice, la variable “x” es independiente, por lo que se puede elegir cualquier numero perteneciente a los números reales y a todos ellos les asignara el mismo valor, 4; por lo que la gráfica es una recta horizontal que corta al eje Y en 4.
Función lineal
Graficar la función g(x)=3x-4, así como determinar su dominio y rango
Parámetros: m=pendiente y B= ordenada en el origen
Utilizando una tabla para encontrar los valores se tiene:
X | g(x)=3x-4 |
-2 | -10 |
-1 | -7 |
0 | -4 |
1 | -1 |
2 | 2 |
3 | 5 |
g(x)=3x-4
g(-2)=3(-2)-4=-10
g(-1)=3(-1)-4=-7
g(-0)=3(-0)-4=-4
g(1)=3(1)-4=-1
g(2)=3(2)-4=2
g(3)=3(3)-4=5
Al tener la función, se puede calcular cualquier valor de X que se desee, enteros, racionales, inclusive los irracionales, por lo tanto se deben unir los puntos mediante una línea recta. Con ello se comprueba que su dominio son los números reales, como se observa a continuación.
Función cuadrática
Graficar la función T(x)=; obtener el dominio y el rango.
|
x | T(x)=X2 + 4x + 1 |
-4 | 1 |
-3 | -2 |
-2 | -3 |
-1 | -2 |
0 | 1 |
1 | 6 |
Su gráfica es:
Función cubica
Graficar la función D(x)=x3 -6X2 + 12x -6; obtener el dominio y el rango.
|
X | D(X)=X3 -6X2 + 12X -6 |
0.5 | -1.375 |
1 | 1 |
1.5 | 1.875 |
2 | 2 |
2.5 | 2.125 |
3 | 3 |
3.5 | 5.375 |
Su gráfica es:
Función cuartica:
Graficar la función f(x)=4X4 -6x3 +2x2 -2x -3; obtener el dominio y el rango.
Se utiliza una tabla para determinar la gráfica de la función.
X | f(x)=4X4 -6x3 +2x2 -2x -3 |
-1 | 11 |
-0.5 | -0.5 |
0 | -3 |
0.5 | -4 |
1 | -5 |
1.5 | -1.5 |
|
Funciones racionales
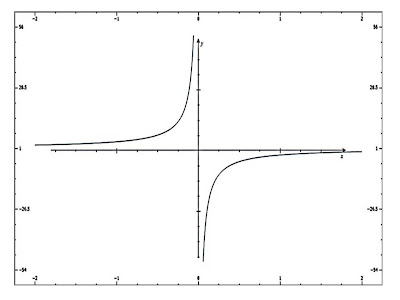
Graficar la función f(x)= x2-4/x+2 ; determinar su dominio y rango
Se utiliza la tabla para conocer algunos de los puntos que pertenecen a la función
X | F(x)=x2-4/x+2 |
-4 | -6 |
-3 | -5 |
-2 | No definido |
-1 | -3 |
0 | -2 |
1 | -1 |
2 | 0 |
|
Al graficar se obtiene:
Como se observa en la gráfica, el comportamiento
de los puntos parece ser una recta, pero cuando la
Variable toma el valor de -2, el cociente tiene divisor
cero, por lo tanto, se indefine. Para poder determinar
el comportamiento alrededor de la indefinición, se
requiere tomar valores cerrados a x=-2.
Funciones Polinomiales.
Graficar esta función, asi como determinar su dominio y rango.
Para resolver este ejemplo, se utiliza una tabla para encontrar las coordenadas de lo puntos.
Al ubicar los puntos en el plano cartesiano se obtiene
“FUNCIONES TRASCENDENTES”
Funciones trigonométrica
Graficar la función f(x)= sen x, determinar su dominio y rango.
X | f(x)= sen x |
-6 | 0.28 |
-4 | 0.76 |
-2 | -0.91 |
0 | 0 |
2 | 0.91 |
4 | -0.76 |
6 | -0.28 |
Al graficar lo puntos se obtiene la gráfica:
Funciones exponenciales
Graficar la función p(x) = -ex + 3, determinar su dominio y rango.
Utilizando una tabla para determinar el comportamiento se tienen los siguientes puntos.
X | p(x) = -ex + 3 |
-5 | 2.0993 |
-4 | 2.982 |
-3 | 2.95 |
-2 | 2.865 |
-1 | 2.9 |
0 | 2 |
1 | 0.282 |
2 | -4.389 |
3 | -17.086 |
Funciones logarítmicas
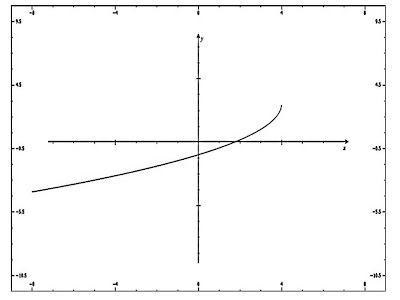
Graficar la función S(x)= Log(-x + 1) +2, determinar su dominio y rango.
Utilizando una tabla para determinar el comportamiento se tienen los siguientes puntos.
X | S(x)= Log(-x + 1) +2 |
-5 | 2.78 |
-4 | 2.70 |
-3 | 2.60 |
-2 | 2.48 |
-1 | 2.30 |
0 | 2 |
0.5 | 1.70 |
0.8 | 1.30 |
0.9 | 1 |
1 | No existe |
2 | No existe |
Su gráfica:
“SEGÚN LA PRESENTACIÓN DE SU FROMA ANÁLITICA”
Funciones explicitas
4x -3y + 8 = 0
-3y 0 -4x -8
y=-4x-8
-3
-3
y=4 x + 8
3 3 ó f(x)=4 x + 8 función lineal
3 3
3 3 ó f(x)=4 x + 8 función lineal
3 3
Funciones implícita
2(3x + 2y) = 6x -4y +8 es una función constante
FUNCIONES CONTINUAS
FUNCIONES DISCONTINUAS
“SEGÚN SU VARIACIÓN”
Funciones creciente y decreciente
Determinar para que intervalos de la función f(x) = 2(x – 2) + 1 es creciente o decreciente
3
3
La función tiene dos comportamientos:
1. A medida que “x” se acerca a 2. La función va decreciendo.
2. Cuando “x” es mayor que 2 la función va creciendo.
Por lo tanto, su función es decreciente en el intervalo:(- ,2)
,2)
La función es creciente en el intervalo: (2, )
)
“SEGÚN LA FORMA DE CORRESPONDENCIA ENTRE SUS CONJUNTOS”
Biyectiva (uno a uno)
Se relaciona las candidatas a reina del primer semestre del colegio de bachilleres de magdalena, con el grupo actual pertenecen.

la relación funcional es Inyectiva debido a que a cada alumna la asocia con su grupo y no existen dos candidatas que pertenezcan al mismo grupo.
SOBREYECTIVA (SOBRE)
La relación funcional de las jóvenes con su clase de danza es Sobreyectiva, dado que en todos los cursos que se ofrecen para danza tiene al menos una alumna de ese conjunto de chicas.
Biyectiva
El retiro matrimonial ofrece la oportunidad a los matrimonios de reforzar su unión y renovar sus votos.
Grupo de esposas grupo deesposos
La relación funcional que existe entre los conjuntos es Biyectiva, puesto que a cada esposa la relaciona con su esposo y a su vez, no existe ningún esposo que haya asistido sin su esposa.
-Hoja de cálculo-
-Se define como un programa diseñado para almacenar, organizar, procesar, presentar y compartir información numérica, textual y grafica.
Elementos importantes:
- Fila
- Título de la fila
- Columna
- Celda
- Rango
-Función matemática-
- En matemática, una función es una relación entre un conjunto dado X y otro conjunto de elementos Y de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio. En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.
Elementos importantes:
- Dominio
- Rango
Para que se usan o de donde se obtienen
Hoja de cálculo:
Se usan para crear gráficas, tablas, nominas estados de cuenta, proyecciones, conversión de monedas, resolver ecuaciones, etc. La hoja de cálculo se suele usar para varias maneras.
Función matemática:
Una función obtiene un valor, pero esto no quiere decir que se obtengan todos los valores que se nos antojen. El conjunto de valores que se obtienen a partir del conjunto de valores del dominio de definición se llama recorrido de la función
EJEMPLOS DE LA VIDA COTIDIANA DE DONDE SE OBTIENEN O SE USAN LAS FUNCIONES MATEMÁTICAS.
Ejemplo 1.
El tanque de gasolina de un automóvil contiene 10 litros. Si su rendimiento es de 12 Km/L, la tabla muestra la cantidad de gasolina contra la distancia, medida de cada 24 km.
LITROS (l) | DISTANCIA (d) |
2 | 24 |
4 | 48 |
6 | 72 |
8 | 96 |
10 | 120 |
En este caso cada columna representa un conjunto por lo que la función se representa de la siguiente forma.
F: L ----> D
Donde L representa al conjunto de litros y D al conjunto de las distancias.
Debido a la descripción del problema y la información que se tiene de la tabla, se puede representar la forma analítica de la función, de hecho, el comportamiento es lineal, a medida que se consumen 2 litros el automóvil avanza 24 kilómetros. Por lo tanto la función quedaría:
F (l)= 12l
Ejemplo 2.
Un taxista cobra 30 pesos por salida y cada 5 pesos por km recorrido. Calcular:
a) a) El costo de un viaje en x kilómetros.
b) b) El costo del viaje si el destino de una persona es de 12 km.
Es claro en el enunciado del problema, que el cobro del viaje depende de la distancia recorrida y se pueden particularizar algunos casos para visualizar la estructura de la función que lo describe.
Si el viaje es de 1 km, su costo es de 30+5(1)=35 pesos.
Si el viaje es de 3 km, su costo es de 30+5(3)=45 pesos.
Si el viaje es de 10 km, su costo es de 30+5(10)=80 pesos.
Generalizando:
Si el viaje es de x km, su costo es de 30+5(x) pesos.
Por lo tanto, la respuesta al inciso “a”, es: C(x)= 30 + 5x
Donde C(x) es el costo del viaje en taxi función de la distancia recorrida “x”.
En el inciso “b” se solicita un costo en particular que es el de 12km, sólo basta sustituir este dato en la función y así encontrar lo que se busca.
C(12) =30 + 5(12) = 90
Por lo tanto, el costo del viaje cuando se recorren 12km es de 90 pesos.
PROBLEMA TEÓRICO
Dada la función f(x) = 5x2 + 2
Encontrar el valor de la función para cuando x = 2.
Para calcular la imagen de un elemento bajo la función f, se reemplaza dicho elemento en el lugar de la variable, así para x = 2
f(2) = 5(2)2 + 2
f(2) = 22
Por lo tanto cuando x = 2, se tiene que f(2) = 22.
PROBLEMA PRÁCTICO
El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.
a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.
b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?
c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?
Veamos:
a) Si llamamos x al número de Km recorridos, la fórmula de la función es f (x) = 15 + 0,2x.
b) x = 50 entonces
f (50) = 15 + 0,2 • 50 = 25
Hay que pagar 25 dólares.
c) f (x) = 53 entonces
15 + 0,2x = 53 entonces x = 190
Se han recorrido 190 km.
Conclusión
Para concluir con este tema nos damos cuenta que las funciones matemáticas no solo las utilizamos para la escuela, sino que también las usamos en nuestra vida cotidiana y sin darnos cuenta, igual y no sea tal cual como se los presentamos despejando la variable x pero si las utilizamos, también nos damos cuenta del cómo nos pueden servir las hojas de cálculo, en ellas vemos que podemos trabajar a gusto y presentaremos un trabajo de calidad. Este tema nos ayudó a comprender aún más la temática de las nuevas tecnologías en nuestra vida ya que las podemos aprovechar al máximo y obtener buenos resultados y no solo por ahorita sino que también en un futuro nos servirá del todo, ya que en todo tipo de trabajo es necesario saber manejar algún tipo de programa y no hay mejor como la hoja de cálculo, esperamos haya sido de su agrado y puedan sacarle provecho a nuestro trabajo.
BÚSQUEDA DE INFORMACIÓN
1.- ¿Cuántas de las páginas Web propuestas en el apartado “Recursos” consultaron?
Utilizamos todas, ya que se necesitaba recaudar información para poder elaborar este trabajo
2.- ¿En cuántas de ellas encontraron información que luego usaron en su trabajo?
La mayoría de ellas, solo que algunas las omitimos ya que era la misma información antes consultada
3.- De los puntos propuestos en la “Tarea”, ¿Cuántos completaron consultando más de una página?
De los cinco puntos fueron tres los que completamos así
TRABAJO EN EQUIPO
1.- ¿La contribución de los elementos del equipo ha sido equilibrada?
Si, ya que a cada quien le toco una parte del trabajo
2.- Cuando había diferentes opiniones sobre cómo desarrollar el trabajo, ¿se ponían fácilmente de acuerdo?
Primero escuchábamos la opinión de cada uno ya que fuera la opinión que tuviera era importante, ya después entre los tres nos poníamos de acuerdo al ver cuál podría ser la más apropiada para nuestro trabajo.
INFORME FINAL
1.- ¿Siguieron todos los pasos indicados en el apartado “Proceso”?
Si, ya que fuera el paso que fuera se tenía que evaluar de acuerdo a lo solicitado
2.- ¿Completaron todos los puntos indicados en el apartado “Tarea”?
Si, ya que queríamos presentar un trabajo completo
3.- ¿Están satisfechos con el trabajo resultante?
Claro, ya que nos dimos cuenta que en equipo es mucho mejor y resulta un trabajo de calidad
4.- ¿Creen que si expusieran su trabajo a otros compañeros lo entenderían bien?
Pues nosotros creemos que sí, ya que es un tema muy común que lo vemos a diario en clases y todos presentaremos información relacionada con esto.

















No hay comentarios:
Publicar un comentario